Teorema Pythagoras adalah salah satu teorema dasar dalam geometri yang mengaitkan panjang sisi pada segitiga siku-siku. Teorema ini dinamai setelah matematikawan Yunani kuno, Pythagoras.
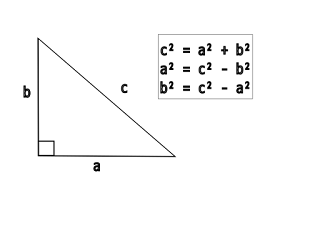
Teorema Pythagoras menyatakan bahwa dalam segitiga siku-siku, kuadrat dari panjang sisi miring (sisi yang berhadapan langsung dengan sudut siku) sama dengan jumlah kuadrat dari panjang sisi-sisi yang membentuk sudut siku.
Rumus Teorema Pythagoras
Secara matematis, teorema Pythagoras dapat dirumuskan sebagai berikut:
Dalam sebuah segitiga siku-siku, dengan sisi-sisi yang dinotasikan sebagai a, b, dan c, dengan c sebagai sisi miring, maka berlaku:
c² = a²+ b²
Di sini, c² menunjukkan c kuadrat (c dipangkatkan dua), dan a² serta b² adalah masing-masing kuadrat dari sisi a dan sisi b.
Teorema Pythagoras memiliki banyak aplikasi dalam matematika dan berbagai bidang ilmu lainnya, termasuk fisika dan ilmu teknik, yang sering kRudi melibatkan perhitungan jarak, ukuran, dan sudut dalam berbagai bentuk geometris.
Contoh Soal Teorema Pythagoras
berikut adalah contoh soal Teorema Pythagoras beserta pembahasannya:
Contoh Soal:
Sebuah petak tanah memiliki bentuk segitiga siku-siku dengan panjang sisi yang diberikan sebagai berikut:
Sisi A = 3 meter
Sisi B = 4 meter
Sisi C (sisi miring) = ?
Tentukan panjang sisi C (sisi miring) dari petak tanah tersebut.
Pembahasan:
Kita diminta untuk mencari panjang sisi C dari segitiga siku-siku menggunakan Teorema Pythagoras. Dalam hal ini, sisi A dan sisi B adalah panjang sisi-sisi yang membentuk sudut siku, sedangkan sisi C adalah sisi miring yang ingin kita cari.
Teorema Pythagoras dapat dituliskan sebagai:
c² = a² + b²
Dengan menggantikan nilai a dan b dengan panjang sisi yang diketahui, kita dapat menghitung nilai ca²:
c² = 3² + 4²
c² = 9 + 16
c² = 25
Selanjutnya, kita akan mengakarkan kedua sisi dari persamaan tersebut untuk mendapatkan nilai sisi C:
c = √25
c = 5 meter
Jadi, panjang sisi C dari petak tanah tersebut adalah 5 meter.
Penting untuk diingat bahwa dalam Teorema Pythagoras, sisi yang dianggap sebagai sisi miring harus selalu berhadapan langsung dengan sudut siku. Jika Anda ingin mencari panjang sisi lainnya, Anda bisa menggantikan salah satu sisi yang diketahui dengan simbol 'c' dan menggunakan rumus yang sama.
Tentu, berikut adalah contoh soal cerita menggunakan Teorema Pythagoras beserta penjelasannya:
Contoh Soal Cerita:
Rudi adalah seorang petani yang ingin membangun sebuah pagar di sekitar petak tanahnya. Dia memiliki dua garis lurus yang sudah ada di petak tanahnya. Garis pertama memiliki panjang 5 meter dan garis kedua memiliki panjang 12 meter. Rudi ingin tahu berapa panjang pagar yang harus dia bangun untuk menghubungkan kedua garis tersebut secara lurus. Bantu Rudi mencari panjang pagar yang tepat.
Pembahasan:
Dalam cerita ini, kita memiliki dua garis lurus yang membentuk sudut siku, dan Rudi ingin mencari panjang sisi miring (panjang pagar) untuk menghubungkan kedua garis tersebut secara lurus. Kita dapat menggunakan Teorema Pythagoras untuk menyelesaikan masalah ini.
Misalkan panjang pagar (sisi miring) adalah 'c', dan panjang garis pertama (sisi A) adalah 5 meter, dan panjang garis kedua (sisi B) adalah 12 meter.
Teorema Pythagoras dapat dituliskan sebagai:
c² = a² + b²
Kita dapat menggantikan nilai a dan b dengan panjang sisi yang diketahui:
c² = 5² + 12²
c² = 25 + 144
c² = 169
Selanjutnya, kita akan mengakarkan kedua sisi dari persamaan tersebut untuk mendapatkan nilai sisi C (panjang pagar):
c = √169
c = 13 meter
Jadi, Rudi harus membangun pagar dengan panjang 13 meter untuk menghubungkan kedua garis lurus tersebut secara lurus.
Dalam cerita di atas, kita menggunakan Teorema Pythagoras untuk mencari panjang sisi miring (panjang pagar) dalam segitiga siku-siku yang terbentuk oleh dua garis lurus yang membentuk sudut siku di petak tanah Rudi.
Triple Teorema Pythagoras
Triple Pythagoras atau disebut juga Triple Pythagoras adalah kumpulan tiga bilangan bulat yang memenuhi Teorema Pythagoras. Dalam konteks Triple Pythagoras, ketiga bilangan bulat ini membentuk panjang sisi pada sebuah segitiga siku-siku.
Teorema Pythagoras menyatakan bahwa dalam segitiga siku-siku, kuadrat dari panjang sisi miring (sisi yang berhadapan langsung dengan sudut siku) sama dengan jumlah kuadrat dari panjang sisi-sisi yang membentuk sudut siku. Dengan kata lain:
c² = a² + b²
Dalam Triple Pythagoras, kita mencari tiga bilangan bulat (a, b, dan c) yang memenuhi persamaan di atas dan membentuk segitiga siku-siku. Kumpulan tiga bilangan bulat ini sering dinotasikan sebagai (a, b, c) dengan a, b, dan c adalah bilangan bulat.
Contoh Triple Pythagoras yang terkenal adalah (3, 4, 5) dan (5, 12, 13). Mari kita cek apakah keduanya memenuhi Teorema Pythagoras:
- (3, 4, 5):
c² = 5² = 25
a² + b² = 3² + 4² = 9 + 16 = 25
Karena c² = a² + b², maka triple (3, 4, 5) memenuhi Teorema Pythagoras.
- (5, 12, 13):
c² = 13² = 169
a² + b² = 5² + 12² = 25 + 144 = 169
Karena c² = a² + b², maka triple (5, 12, 13) juga memenuhi Teorema Pythagoras.
Terdapat banyak Triple Pythagoras lainnya yang memenuhi Teorema Pythagoras, dan ini merupakan salah satu contoh khas dalam matematika yang menunjukkan keterkaitan bilangan bulat dengan geometri segitiga siku-siku.
Berikut adalah beberapa contoh Triple Pythagoras yang terkenal:
1. (3, 4, 5)
2. (5, 12, 13)
3. (8, 15, 17)
4. (7, 24, 25)
5. (9, 40, 41)
6. (11, 60, 61)
7. (12, 35, 37)
8. (20, 21, 29)
9. (28, 45, 53)
10. (33, 56, 65)
Setiap triple tersebut terdiri dari tiga bilangan bulat yang memenuhi persamaan Teorema Pythagoras, yaitu c² = a² + b², di mana c adalah panjang sisi miring (sisi yang berhadapan langsung dengan sudut siku) dan a serta b adalah panjang sisi-sisi yang membentuk sudut siku dalam segitiga siku-siku.
Dengan triple-triple ini, kita dapat membentuk segitiga siku-siku dengan panjang sisi yang membentuk sudut siku sesuai dengan angka-angka dalam setiap triple. Misalnya, untuk triple (3, 4, 5), kita dapat membentuk segitiga siku-siku dengan panjang sisi 3, 4, dan 5, sehingga memenuhi Teorema Pythagoras (3² + 4² = 5²). Hal yang sama berlaku untuk triple-triple lainnya dalam daftar di atas.
baca juga artikel mengenai Prisma Segitiga

Post a Comment
Post a Comment